pre-tenuring in v8
Hey hey happy new year, friends! Today I was going over some V8 code that touched pre-tenuring: allocating objects directly in the old space instead of the nursery. I knew the theory here but I had never looked into the mechanism. Today’s post is a quick overview of how it’s done.
allocation sites
In a JavaScript program, there are a number of source code locations that allocate. Statistically speaking, any given allocation is likely to be short-lived, so generational garbage collection partitions freshly-allocated objects into their own space. In that way, when the system runs out of memory, it can preferentially reclaim memory from the nursery space instead of groveling over the whole heap.
But you know what they say: there are lies, damn lies, and statistics. Some programs are outliers, allocating objects in such a way that they don’t die young, or at least not young enough. In those cases, allocating into the nursery is just overhead, because minor collection won’t reclaim much memory (because too many objects survive), and because of useless copying as the object is scavenged within the nursery or promoted into the old generation. It would have been better to eagerly tenure such allocations into the old generation in the first place. (The more I think about it, the funnier pre-tenuring is as a term; what if some PhD programs could pre-allocate their graduates into named chairs? Is going straight to industry the equivalent of dying young? Does collaborating on a paper with a full professor imply a write barrier? But I digress.)
Among the set of allocation sites in a program, a subset should pre-tenure their objects. How can we know which ones? There is a literature of static techniques, but this is JavaScript, so the answer in general is dynamic: we should observe how many objects survive collection, organized by allocation site, then optimize to assume that the future will be like the past, falling back to a general path if the assumptions fail to hold.
my runtime doth object
The high-level overview of how V8 implements pre-tenuring is based on per-program-point AllocationSite objects, and per-allocation AllocationMemento objects that point back to their corresponding AllocationSite. Initially, V8 doesn’t know what program points would profit from pre-tenuring, and instead allocates everything in the nursery. Here’s a quick picture:
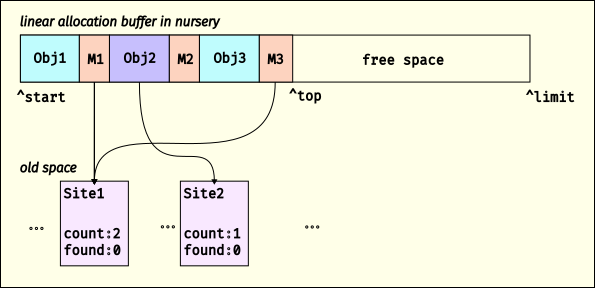
Here we show that there are two allocation sites, Site1 and Site2. V8 is currently allocating into a linear allocation buffer (LAB) in the nursery, and has allocated three objects. After each of these objects is an AllocationMemento; in this example, M1 and M3 are AllocationMemento objects that point to Site1 and M2 points to Site2. When V8 allocates an object, it increments the “created” counter on the corresponding AllocationSite (if available; it’s possible an allocation comes from C++ or something where we don’t have an AllocationSite).
When the free space in the LAB is too small for an allocation, V8 gets another LAB, or collects if there are no more LABs in the nursery. When V8 does a minor collection, as the scavenger visits objects, it will look to see if the object is followed by an AllocationMemento. If so, it dereferences the memento to find the AllocationSite, then increments its “found” counter, and adds the AllocationSite to a set. Once an AllocationSite has had 100 allocations, it is enqueued for a pre-tenuring decision; sites with 85% survival get marked for pre-tenuring.
If an allocation site is marked as needing pre-tenuring, the code in which it is embedded it will get de-optimized, and then next time it is optimized, the code generator arranges to allocate into the old generation instead of the default nursery.
Finally, if a major collection collects more than 90% of the old generation, V8 resets all pre-tenured allocation sites, under the assumption that pre-tenuring was actually premature.
tenure for me but not for thee
What kinds of allocation sites are eligible for pre-tenuring? Sometimes it depends on object kind; wasm memories, for example, are almost always long-lived, so they are always pre-tenured. Sometimes it depends on who is doing the allocation; allocations from the bootstrapper, literals allocated by the parser, and many allocations from C++ go straight to the old generation. And sometimes the compiler has enough information to determine that pre-tenuring might be a good idea, as when it generates a store of a fresh object to a field in an known-old object.
But otherwise I thought that the whole AllocationSite mechanism would apply generally, to any object creation. It turns out, nope: it seems to only apply to object literals, array literals, and new Array. Weird, right? I guess it makes sense in that these are the ways to create objects that also creates the field values at creation-time, allowing the whole block to be allocated to the same space. If instead you make a pre-tenured object and then initialize it via a sequence of stores, this would likely create old-to-new edges, preventing the new objects from dying young while incurring the penalty of copying and write barriers. Still, I think there is probably some juice to squeeze here for pre-tenuring of class-style allocations, at least in the optimizing compiler or in short inline caches.
I suspect this state of affairs is somewhat historical, as the AllocationSite mechanism seems to have originated with typed array storage strategies and V8’s “boilerplate” object literal allocators; both of these predate per-AllocationSite pre-tenuring decisions.
fin
Well that’s adaptive pre-tenuring in V8! I thought the “just stick a memento after the object” approach is pleasantly simple, and if you are only bumping creation counters from baseline compilation tiers, it likely amortizes out to a win. But does the restricted application to literals point to a fundamental constraint, or is it just accident? If you have any insight, let me know :) Until then, happy hacking!