type folding in guile
A-hey hey hey, my peeps! Today's missive is about another optimization pass in Guile that we call "type folding". There's probably a more proper name for this, but for the moment we go with "type folding" as it's shorter than "abstract constant propagation, constant folding, and branch folding based on flow-sensitive type and range analysis".
on types
A word of warning to the type-system enthusiasts among my readers: here I'm using "type" in the dynamic-languages sense, to mean "a property about a value". For example, whether a value is a vector or a pair is a property of that value. I know that y'all use that word for other purposes, but there are other uses that do not falute so highly, and it's in the more pedestrian sense that I'm interested here.
To back up a bit: what are the sources of type information in dynamic languages? In Guile, there are three ways the compiler can learn about a value's type.
One source of type information is the compiler's knowledge of the result types of expressions in the language, especially constants and calls to the language's primitives. For example, in the Scheme definition (define y (vector-length z)), we know that y is a non-negative integer, and we probably also know a maximum value for z too, given that vectors have a maximum size.
Conditional branches with type predicates also provide type information. For example, in consider this Scheme expression:
(lambda (x)
(if (pair? x)
(car x)
(error "not a pair" x)))
Here we can say that at the point of the (car x) expression, x is definitely a pair. Conditional branches are interesting because they add a second dimension to type analysis. The question is no longer "what is the type of all variables", but "what is the type of all variables at all points in the program".
Finally, we have the effect of argument type checks in function calls. For example in the (define y (vector-length z)) definition, after (vector-length z) has been evaluated, we know that z is indeed a vector, because if it weren't, then the primitive call would raise an exception.
In summary, the information that we would like to have is what type each variable has at each program point (label). This information comes from where the variables are defined (the first source of type information), conditional branches and control-flow joins (the second source), and variable use sites that imply type checks (the third). It's a little gnarly but in essence it's a classic flow analysis. We treat the "type" of a variable as a set of possible types. A solution to the flow equations results in a set of types for each variable at each label. We use the intmap data structures to share space between the solution at different program points, resulting in an O(n log n) space complexity.
In Guile we also solve for the range of values a variable may take, at the same time as solving for type. I started doing this as part of the Compost hack a couple years ago, where I needed to be able to prove that the operand to sqrt was non-negative in order to avoid sqrt producing complex numbers. Associating range with type turns out to generalize nicely to other data types which may be thought of as having a "magnitude" -- for example a successful (vector-ref v 3) implies that v is at least 4 elements long. Guile can propagate this information down the flow graph, or propagate it in the other way: if we know the vector was constructed as being 10 elements long, then a successful (vector-ref v n) can only mean that n is between 0 and 9.
what for the typing of the things
Guile's compiler uses type analysis in a few ways at a few different stages. One basic use is in dead code elimination (DCE). An expression can be eliminated from a program if its value is never used and if it causes no side effects. Guile models side effects (and memory dependencies between expressions) with effects analysis. I quote:
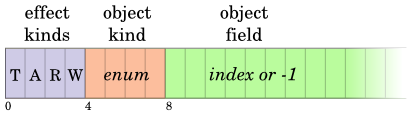
We model four kinds of effects: type checks (T), allocations (A), reads (R), and writes (W). Each of these effects is allocated to a bit. An expression can have any or none of these effects.
In an expression like (vector-ref v n), type analysis may compute that in fact v is indeed a vector and n is an integer, and also that n is within the range of valid indexes of v. In that case we can remove the type check (T) bit from the expression's effects, opening up the expression for DCE.
Getting back to the topic of this article, Guile's "type folding" pass uses type inference in three ways.
The first use of type information is if we determine that, at a given use site, a variable has precisely one type and one value. In that case we can do constant folding over that expression, replacing its uses with its value. For example, let's say we have the expression (define len (vector-length v)). If we know that v is a vector of length length 5, we can replace any use of len with the constant, 5. As an implementation detail we actually keep the definition of len in place and let DCE remove it later. We can consider this to be abstract constant propagation: abstract in the sense that it folds over abstract values, represented just as type sets and ranges, and which materializes a concrete value only if it is able to do so. Since ranges propagate through operators as well, it can also be considered as abstract constant folding; the type inference operators act as constant folders.
Another use of type information is in branches. If Guile sees (if (< n (vector-length v)) 1 2) and n and v have the right types and disjoint ranges, then we can fold the test and choose 1 or 2 depending on how the test folds.
Finally type information can enable strength reduction. For example it's a common compiler trick to want to reduce (* n 16) to (ash n 4), but if n isn't an integer this isn't going to work. Likewise, (* n 0) can be 0, 0.0, 0.0+0.0i, something else, or an error, depending on the type of n and whether the * operator has been extended to apply over non-number types. Type folding uses type information to reduce the strength of operations like these, but only where it can prove that the transformation is valid.
So that's type folding! It's a pretty neat pass that does a few things as once. Code here, and code for the type inference itself here.
type-driven unboxing
Guile uses type information in one other way currently, and that is to determine when to unbox floating-point numbers. The current metric is that whenever an arithmetic operation will produce a floating-point number -- in Scheme parlance, an inexact real -- then that operation should be unboxed, if it has an unboxed counterpart. Unboxed operations on floating-point numbers are advantageous because they don't have to allocate space on the garbage-collected heap for their result. Since an unboxed operation like the fadd floating-point addition operator takes raw floating-point numbers as operands, it also will never cause a type check, unlike the polymorphic add instruction. Knowing that fadd has no effects lets the compiler do a better job at common subexpression elimination (CSE), dead code elimination, loop-invariant code motion, and so on.
To unbox an operation, its operands are unboxed, the operation itself is replaced with its unboxed counterpart, and the result is then boxed. This turns something like:
(+ a b)
into:
(f64->scm (fl+ (scm->f64 a) (scm->f64 b)))
You wouldn't think this would be an optimization, except that the CSE pass can eliminate many of these conversion pairs using its scalar elimination via fabricated expressions pass.
A proper flow-sensitive type analysis is what enables sound, effective unboxing. After arithmetic operations have been unboxed, Guile then goes through and tries to unbox loop variables and other variables with more than one definition ("phi' variables, for the elect). It mostly succeeds at this. The results are great: summing a packed vector of 10 million 32-bit floating-point values goes down from 500ms to 130ms, on my machine, with no time spent in the garbage collector. Once we start doing native compilation we should be up to about 5e8 or 10e8 floats per second in this microbenchmark, which is totally respectable and about what gcc's -O0 performance gets.
weaknesses
This kind of type inference works great in tight loops, and since that's how many programs spend most of their time, that's great. Of course, this situation is also a product of programmers knowing that tight loops are how computers go the fastest, or at least of how compilers do the best on their code.
Where this approach to type inference breaks down is at function boundaries. There are no higher-order types and no higher-order reasoning, and indeed no function types at all! This is partially mitigated by earlier partial evaluation and contification passes, which open up space in which the type inferrer can work. Method JIT compilers share this weakness with Guile; tracing JIT runtimes like LuaJIT and PyPy largely do not.
up summing
So that's the thing! I was finally motivated to dust off this draft given the recent work on unboxing in a development branch of Guile. Happy hacking and we promise we'll actually make releases so that you can use it soon soon :)
2 responses
Comments are closed.
It’s really cool how different topics are coming together here. “this does not look like an optimization, but it enables this optimization I wrote about a few months ago” ← yay!
These blog posts on the innards of the guile compiler are great. It would nice to see them become part of the official guile manual.